背景介绍
深度学习的威力众所周知,但其模型训练过程常伴随着繁琐的挑战。许多人在深度学习的实践中都曾遇到过各种问题,这些问题使得理想模型的训练变得更加复杂。本文将以理论结合实践的方式,探讨深度学习训练过程中常见的问题及相应解决方案,主要涉及以下几个方面:
- 梯度消失与梯度爆炸
- 收敛速度缓慢
- 过拟合
梯度消失与梯度爆炸
是什么(What)
深度学习中模型参数的更新主要使用 梯度下降法,而基于梯度下降法的公式简化如下 w -= η * ∂loss/∂w,其中 η 为学习率常量,∂loss/∂w 就是 w 参数对应的梯度。
可以看出,训练过程中参数变化多少主要由梯度决定。理想情况下,我们期望训练达到收敛之前梯度值处于合理范围内,不会过小导致参数基本没有更新,也不会太大导致参数反复震荡。但是事实上这两种情况都会出现,对应的就是梯度消失和梯度爆炸。
梯度消失指的是在反向传播过程中,梯度逐渐变得非常小,甚至接近于零。这样的情况下,权重更新几乎不会发生,导致神经网络无法学到有效的特征表示。
梯度爆炸是指在反向传播中,梯度变得非常大,导致权重更新过大,网络变得不稳定。这可能导致权重值趋向于无穷大,使网络无法收敛或者产生不稳定的行为。
为什么(Why)
梯度消失和梯度爆炸的存在与 链式法则 的存在有很大的关系。梯度反向传播是从输出层向输入层传递的,在传递过程中,梯度逐层相乘,如果每层的梯度都小于 1,那么在靠近输入层的地方,梯度可能会变得非常接近于零,此时就会出现梯度消失。
同理而言,各层梯度值都比较大,那么相乘导致最终输入层的梯度就会过大,此时就会出现梯度爆炸。
怎么办(How)
对于梯度消失与梯度爆炸的研究比较久了,因此存在着各种各样的解决方案:
- 权重初始化,使用随机值 或 0 去初始化权重很容易导致梯度消失和爆炸,使用特定方式初始化权重可以避免这个问题,可以考虑使用 Xavier 或 He 初始化方法;
- 批量归一化(Batch Normalization),通过对每层的输入进行标准化,提高了网络的数值稳定性;
- 梯度裁剪(Gradient Clipping),通过设定一个阈值,当梯度的模大于这个阈值时,会将梯度裁剪到这个阈值以内,可以避免梯度爆炸;
- 改变激活函数,选择非饱和的激活函数,如 ReLU 以及其变体;
- 使用 ResNet 残差网络;
动手实践
这边手工构造了一个类似 MLP 的神经网络模型,为了方便查看梯度消失现象,模型的权重初始化为 1:
import torch
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, num_layers, activation_func):
super(MLP, self).__init__()
layers = []
for _ in range(num_layers):
layers.append(nn.Linear(1, 1, bias=False))
layers.append(activation_func())
self.model = nn.Sequential(*layers)
self.initialize()
def forward(self, x):
return self.model(x)
# 初始化模型权重, 初始化为 1.0
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.constant_(m.weight.data, 1.0)
接下来使用下面的方法进行训练 30 层的神经网络(每一层包含一个线性层与一个激活函数),使用的激活函数为 Sigmoid, 对应实现如下所示:
def train(num_layers, activation_func):
model = MLP(num_layers, activation_func)
output = model(torch.tensor([1.0]))
loss = torch.sum(output)
loss.backward()
# 打印每一层的梯度
for name, param in model.named_parameters():
if param.requires_grad:
print(f"{name} grad: {param.grad.item()}")
train(30, nn.Sigmoid)
反向传播后打印的梯度如下所示:
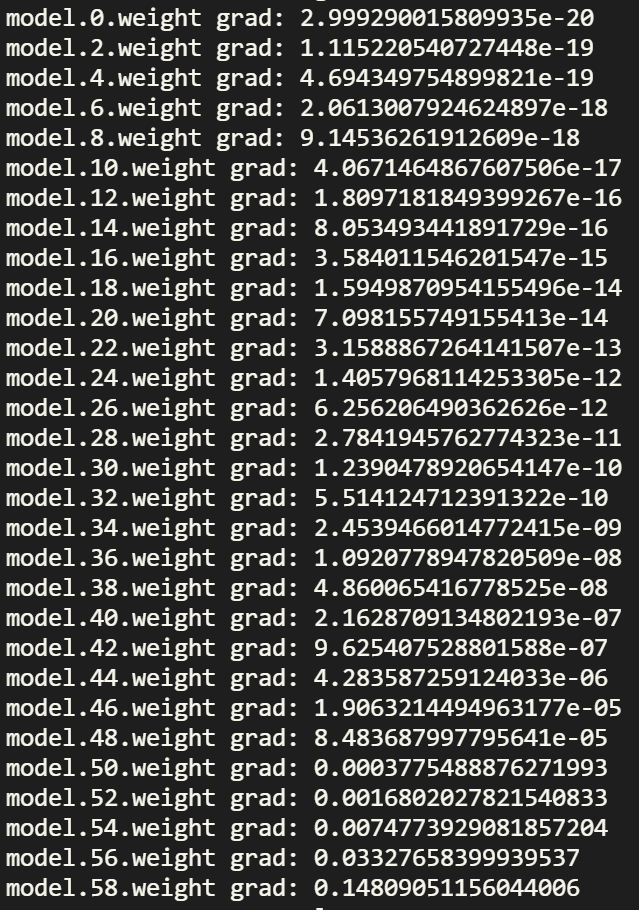
层数是按照数值从小往大递增的,可以看到越靠近输出层的梯度越大,比如最后一层 model.58.weight 的梯度为 0.148,但是越靠近输入层梯度越小,比如第一层 model.0.weight 的梯度为 2.99 * e-20,基本接近 0,表现出梯度消失的特征。
为了解决梯度消失的问题,尝试将激活函数切换为 ReLU, 此时执行的方法为 train(30, nn.ReLU) 对应的梯度如下所示:
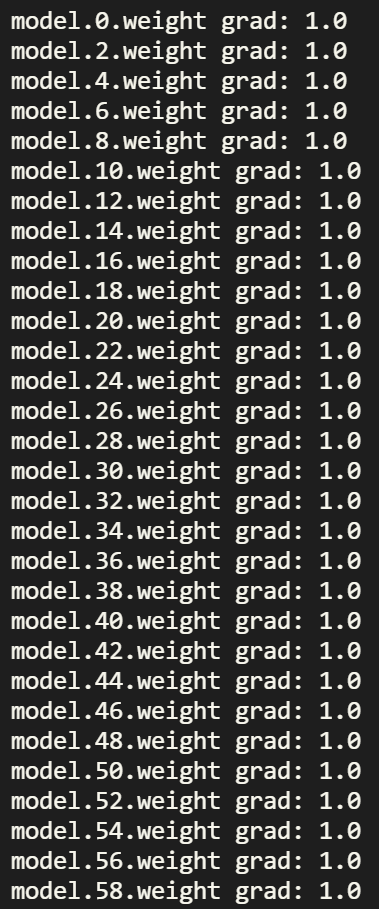
可以看到始终保持在 1.0,梯度消失的现象没有再出现。
为啥切换就梯度消失就不见了呢?事实上,Sigmoid 激活函数对应的导数(梯度)取值范围为 0 ~ 0.25,因此不考虑线性层的情况下,30 层 Sigmoid 梯度的乘积就会导致梯度下降至极小的范围内了,而 ReLU 对应的导数(梯度)为 1,对于反向传播的梯度没有任何影响,因此梯度就不会逐层下降了。
收敛速度慢
是什么(What)
模型收敛是指损失值不再显著下降,参数更新幅度较小,此时模型进入稳定状态。
收敛速度慢是指模型达到稳定状态下的耗时过长。
为什么(Why)
收敛速度慢的原因有很多,常见的原因如下:
- 学习率设置不当可能会导致训练不稳定或收敛速度缓慢。过大的学习率可能会导致训练震荡,过小的学习率可能会导致收敛速度缓慢。
- 权重初始化不当可能会导致需要训练更多轮才能收敛。
- 模型过于复杂可能会导致需要更多的数据用于训练,也会消耗更长的时间才能收敛。
怎么办(How)
- 调整学习率,使其保持在合适的范围内。如果模型损失值下降速度过慢,可以适当提高学习率;如果模型损失值开始震荡或增加,可以考虑适当降低学习率。
- 使用合适的权重初始化方法,比如 Xavier 或 He 初始化。
- 使用更简单的模型结构。
- 使用 ResNet 残差网络结构。
动手实践
直接使用上面提到的神经网络模型 MLP,使用下面的方法生成对应的数据集并进行模型训练:
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
def generate_dataset(num_samples):
torch.manual_seed(42)
X = torch.rand(num_samples, 1)
y = 3 * X + 2 + 0.1 * torch.randn(num_samples, 1)
return X, y
def plot_loss(losses, learning_rate):
plt.plot(losses)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title(f'Training Loss Curve ({learning_rate})')
plt.show()
def train(num_epochs, learning_rate):
losses = []
model = MLP(3, nn.ReLU)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
X_train, y_train = generate_dataset(100)
for epoch in range(num_epochs):
model.train()
y_pred = model(X_train)
loss = criterion(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses.append(loss.item())
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')
plot_loss(losses, learning_rate)
return losses
首先基于较小的学习率 0.001 进行训练,调用 train(500, 0.001) 进行训练,损失值变化如下图所示:
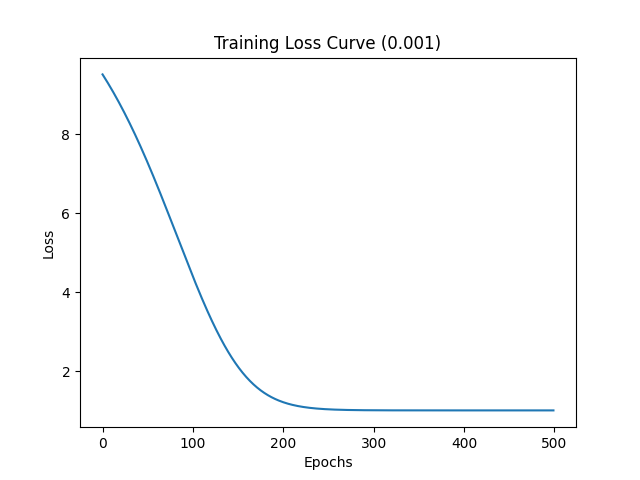
可以看到接近 200 个 Epochs 时模型开始收敛,收敛速度比较慢
为了加速模型训练,将学习率增加至 0.1,损失值变化如下所示:
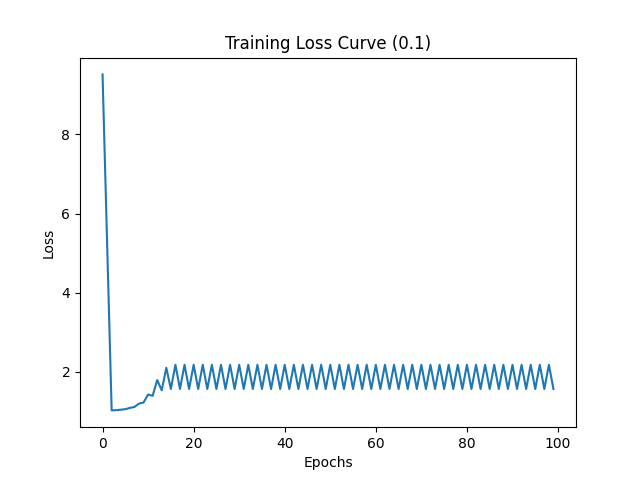
可以看到学习率过大导致损失下降后又开始上升,最后持续震荡,无法收敛。希望加快反而更慢,甚至无法收敛
接下来将学习率调整为 0.01,损失值变化如下所示:
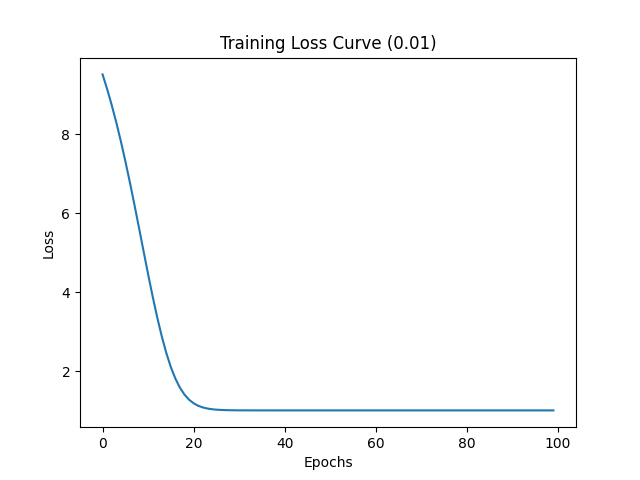
可以看到 20 个 Epochs 时模型就开始收敛,收敛速度加快了很多。
过拟合
是什么(What)
过拟合是指训练误差和测试误差之间的差距太大。一般是模型在训练集上表现很好,但在测试集上却表现很差。模型对训练集”死记硬背”,没有理解数据背后的规律,泛化能力差。
为什么(Why)
过拟合的发生是因为模型过于复杂,以至于学习到了训练数据中的噪声和细节,而无法很好地泛化到新数据上。
怎么办(How)
在深度学习中解决过拟合的手段如下所示:
- 正则化:正则化是通过在损失函数中添加惩罚项来限制模型参数的大小,防止其过于复杂。常见的正则化方法包括 L1 正则化和 L2 正则化;
- Dropout:在训练过程中随机丢弃一些神经元,以减少模型对某些特定神经元的依赖,有助于防止过拟合;
- 更多的数据:提供更多的训练数据可以减轻过拟合,但是获取的数据的一般意味着更高的成本,所以一般使用数据增强手段增加数据;
动手实践
为了构造过拟合的情况,定义了一个模型参数较多的模型,模型定义如下所示:
import torch
import torch.nn as nn
class OverfittingModel(nn.Module):
def __init__(self):
super(OverfittingModel, self).__init__()
self.fc1 = nn.Linear(20, 100)
self.fc2 = nn.Linear(100, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.sigmoid(self.fc2(x))
return x
接下来构造分类数据集,其中包含 1000 条数据,并将 20% 的数据划分为测试集,保留 80% 作为训练数据集:
import torch
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
def generate_dataset():
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32)
return X_train, y_train, X_test, y_test
基于上面的数据集与模型,使用下面的方法进行模型训练,训练完成后比较模型在训练集与测试集上的准确率:
def train(weight_decay=0):
model = OverfittingModel()
criterion = nn.BCELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01, weight_decay=weight_decay)
X_train, y_train, X_test, y_test = generate_dataset()
epochs = 400
for epoch in range(epochs):
outputs = model(X_train)
loss = criterion(outputs, y_train.view(-1, 1))
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (epoch+1) % 10 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# 在训练集和测试集上评估模型
with torch.no_grad():
train_accuracy = ((model(X_train) > 0.5).float() == y_train.view(-1, 1)).float().mean().item()
test_accuracy = ((model(X_test) > 0.5).float() == y_test.view(-1, 1)).float().mean().item()
print(f'Training Accuracy: {train_accuracy:.4f}, Testing Accuracy: {test_accuracy:.4f}')
实际调用 train() 方法完成 400 轮模型训练,结果如下所示:
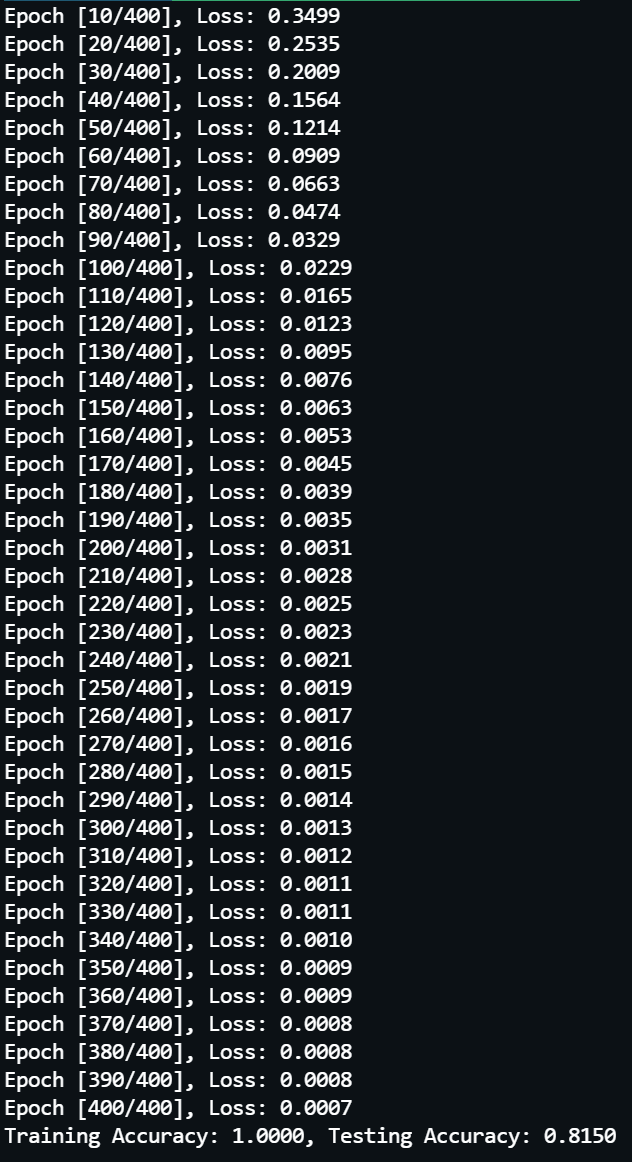
可以看到模型在训练集上表现良好,训练损失值下降至 0.0007,而且准确率为 100%,但是在测试集上表现很差,准确率只有 81.5%。这是明显的过拟合。
为了解决上面的问题,通过设置权重衰减(weight decay)来实现 L2 正则化,实际执行 train(weight_decay=0.04),最终结果如下所示:
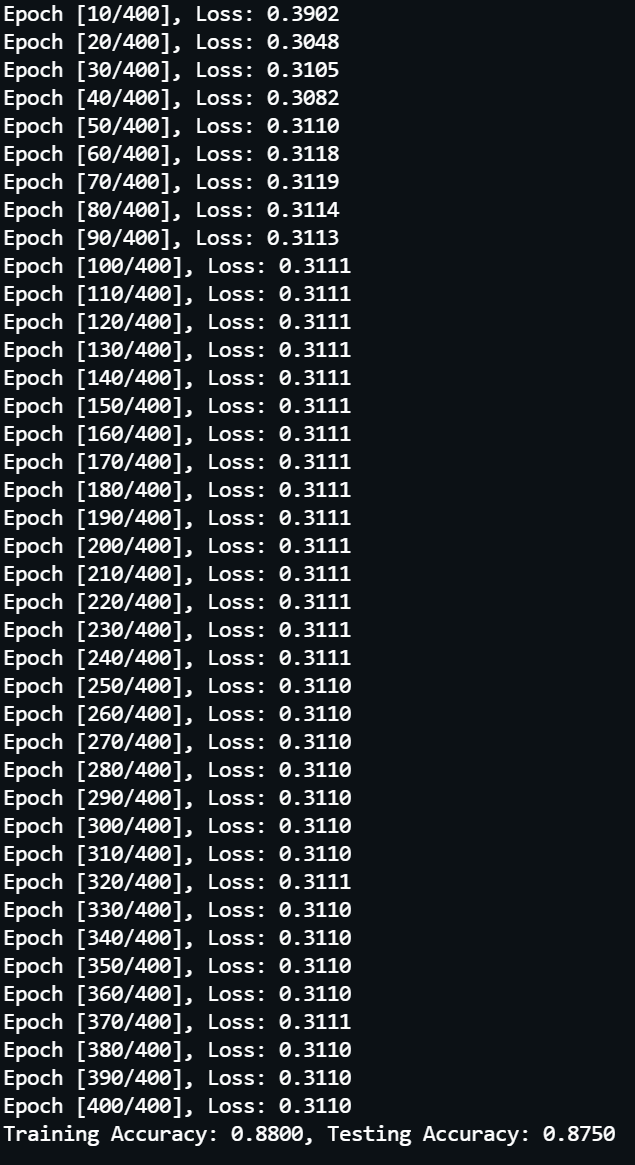
可以看到增加 L2 正则化后在 100 轮左右实现了收敛,在训练接上准确率下降至 88.0%,但是在测试集上准确率提升至 87.5%, 过拟合的问题得到了极大的缓解。
总结
本文总结了深度学习训练过程中常见的几种问题以及常规的解决方案,并通过实践动手定位深度学习问题,同时可以看到解决方案带来的效果改善。本文希望帮助大家建立对深度学习的直观了解,并为深度学习模型的训练提供参考。
深度学习是一门持续发展的学科,正是建立在很多人的研究基础上,深度学习才得以持续发展。一个又一个训练难题得到妥善的解决,最终我们能从几层神经网络,增加至几十层,几百层,甚至得到类似 chatGPT 这样的庞然大物。致敬在这个过程中做出贡献的广大先驱们。