背景介绍
在之前的 FATE 纵向联邦学习实现探索 中介绍了纵向联邦神经网络实现的方案,但是神经网络模型比较复杂,整体的流程也会更复杂,很难简单呈现一个基础的安全纵向联邦的设计思想。因此以纵向联邦线性回归为例,去除与基础纵向联邦无关的部分,由浅入深介绍一个最简化的安全纵向联邦的设计方案。
纵向联邦线性回归
纵向联邦基础思想
前面的 联邦学习下线性回归算法实现概述 中介绍了如何实现最简单的横向联邦学习,横向联邦学习本质上是在各个拥有数据的参与方构建一个独立的小模型,然后将各方的小模型进行聚合得到更好的模型参数,从而得到更好的模型。
可以简单举例,横向联邦中三个拥有数据的参与方各自训练出一个本地的线性回归模型。参与方 1 本地模型为 y1 = w1 * x, 参与方 2 本地模型为 y2 = w2 * x,参与方 3 本地模型为 y3 = w3 * x,最终聚合生成的模型为 y = (w1 + w2 + w3)/3 * x,平均后得到的参数 (w1 + w2 + w3)/3 体现了各个参与方数据的情况,往往表现更好。
而纵向联邦的思路就存在很大差异,因为纵向联邦面临是各方数据的特征是不一致的,因此不能直接聚合得到的更好的模型。但是可以组合生成更大的模型,这样能体现出各方的数据特征对结果的影响。利用更多的特征往往可以训练出更好效果的模型。
举例而言,纵向联邦中三个拥有数据的参与方各自拥有一部分特征,联合训练预测用户的消费能力。参与方 1 拥有的数据 x1 为用户的房子估值训练出本地模型 y1 = w1 * x1, 参与方 2 拥有的数据 x2为用户车子估值训练出本地模型 y2 = w2 * x2,参与方 3 拥有的是用户的收入x3 训练出本地模型 y3 = w3 * x3。最终纵向联邦组合生成的模型为 y = w1 * x1 + w2 * x2 + w3 * x3。最终的模型使用了各方所有数据的特征,拥有比各自本地模型更好的效果。
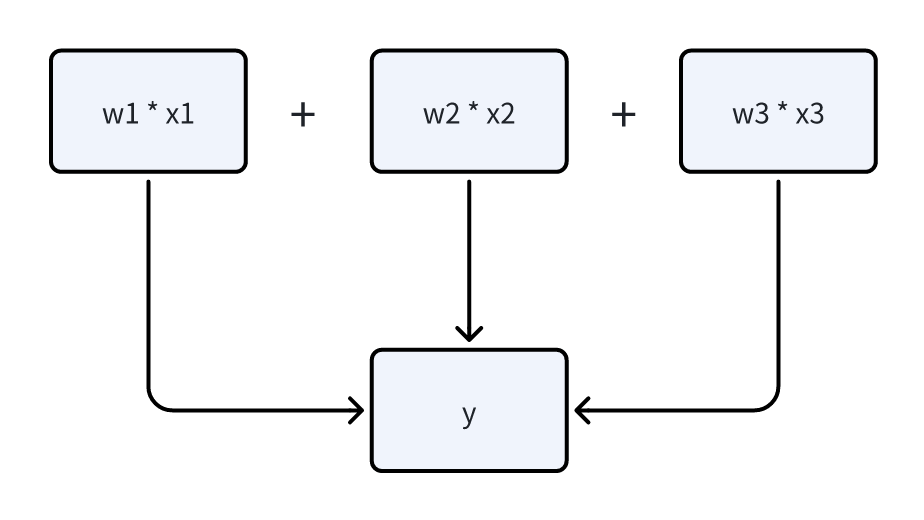
纵向联邦训练流程
继续以上面的例子进行介绍,最终的模型为 y = w1 * x1 + w2 * x2 + w3 * x3,因此前向传播的实现十分简单,直接将各方计算的结果进行累加即可。接下来主要关注反向传播的过程。
线性回归对应的损失函数为 loss = (y_pred - y)^2,其中 y_pred就是前向传播计算的结果,y 就是对应的标签数据。接下来根据链式法则确定各个参数对应梯度:
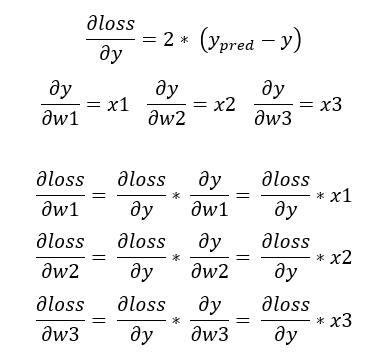
从上面的公式可以看到,最核心的梯度 ∂loss/∂y 是整体的基础。后续参与方对应的参数 w1, w2, w3 计算梯度时,只需要在 ∂loss/∂y 基础上乘上各自的输入 x 即可
在纵向联邦中,只有一个参与方会存在对应的标签数据 y, 根据 FATE 中常规约定,我们将拥有标签数据的参与方叫 Guest, 没有标签数据的参与方叫 Host。根据上面的描述,可以总结出纵向联邦线性回归的流程应该是:
- 前向传播,各个 Host 参与方将计算本地模型的结果
w * x发送给 Guest 参与方,Guest 参与方将各个 Host 参与方发来的结果与 Host 自己本地模型计算的结果直接求和,得到前向传播的预测值y_pred = w1 * x1 + w2 * x2 + w3 * x3; - 反向传播,Guest 计算梯度
∂loss/∂y, 根据上面的公式可以知道∂loss/∂y = 2 * (y_pred - y),然后将计算的梯度下发给各个 Host。各个 Host 与 Guest 自己利用收到的∂loss/∂y乘上自己本次的输入x得到自己本地参数w对应的梯度∂loss/∂w,然后通过w -= η * ∂loss/∂w进行参数w的更新 (η代表学习率常量)。
安全纵向联邦
通过前面过程可以看到实现纵向联邦的过程十分简单,但是这个过程中存在一些明文的数据传递,容易导致敏感数据泄露:
- Host 参与方前向传播的结果
w*x直接明文传递给 Guest; - Guest 反向传播的梯度
∂loss/∂y直接明文传递给 Host;
为了解决上面的问题,可以使用同态加密对数据直接加密,根据目前常规定义方式,同态加密后的结果使用 [] 进行表示。
前向传播中,Host 在发送前向传播的结果给 Guest 之前,先执行同态加密, 实际发送的是加密后的结果 [w*x], 而 Guest 获取到对应的对应的结果后,计算得到同态加密后的预测值 [y_pred] = [w1 * x1] + [w2 * x2] + [w3 * x3]。
反向传播中,计算梯度也是加密后的结果 [∂loss/∂y] = 2 * ([y_pred] - y),此结果发回给 Host 参与方,参与方乘上输入 x 得到加密后的梯度 [∂loss/∂w] = [∂loss/∂y] * x,之后将 [∂loss/∂w] 进行解密,即可得到 w 对应的明文梯度 ∂loss/∂w,使用此值进行参数 w 的更新。
FATE 纵向联邦线性回归
参考 FATE 官方文档 ,FATE 纵向联邦线性回归的流程如下所示:
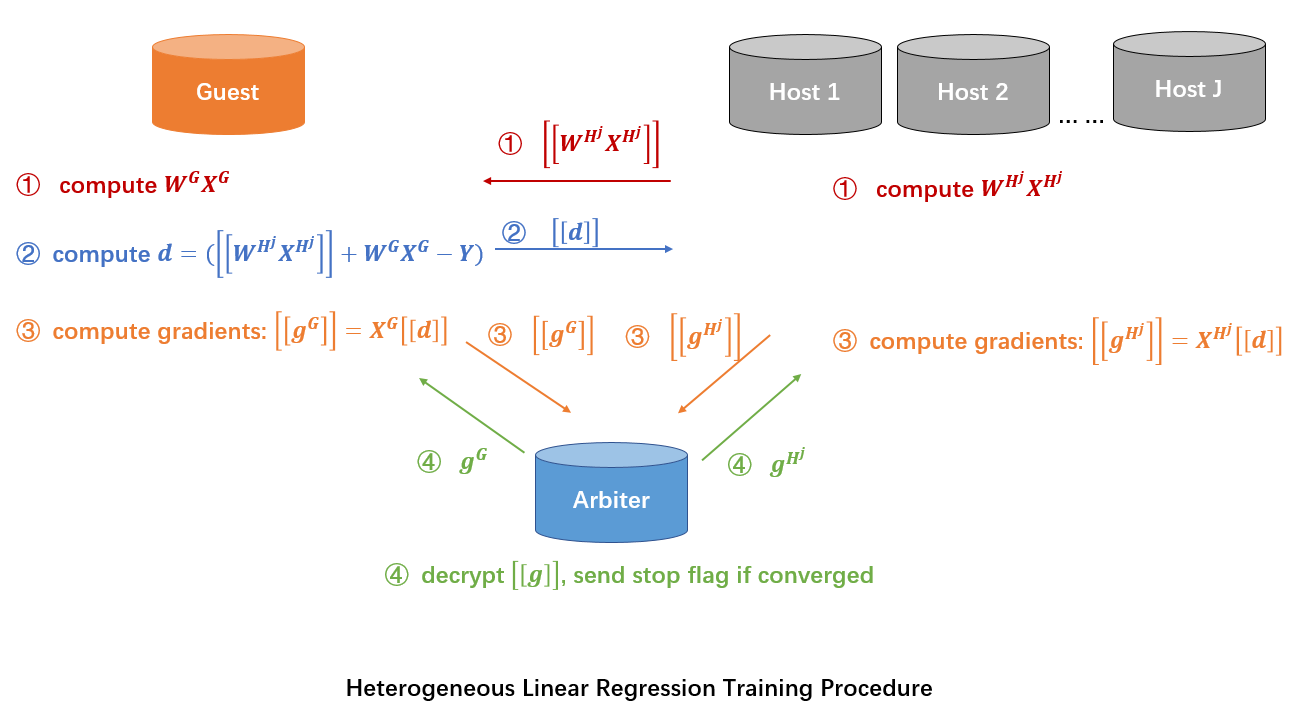
可以看到主要涉及到三种类型的参与方:
- Host 代表有数据但是没有标签文件的参与方,在任务中主要执行本地模型的训练与更新
- Guest 代表有标签文件的参与方,执行本地模型训练,以及反向传播梯度
∂loss/∂y的构造与分发 - Arbiter 代表用于协调的中立第三方,主要用于生成同态加密的密钥对,执行秘钥解密。在判断收敛情况可以提前终止训练
FATE 完整的实现流程如下:
- Arbiter 参与方生成同态加密公钥与私钥,将公钥发送给 Guest 和 Host 参与方(准备阶段,上面图示没有显式标出);
- Host 参与方计算前向传播的结果
W_Hj * X_Hj,使用公钥执行加密得到[W_Hj * X_Hj]发送给 Guest 参与方(前向传播阶段); - Guest 参与方收到所有 Host 参与方前向传播的结果,与本地数据前向传播的结果进行累加。减去标签数据
Y得到 y 反向传播的梯度d = ([W_Hj * X_Hj] + W_G * X_G - Y),并发送结果至 Host 参与方(反向传播阶段,与上面主要差异在于没有乘上 2,常数倍伸缩不影响模型最终结果); - Guest 与 Host 根据 y 反向传播的梯度
[d]计算 w 对应的梯度[g] = x * [d],将 w 反向传播的梯度[g]发送至 Arbiter 进行解密(反向传播阶段); - Arbiter 将解密的梯度
g发送给 Guest 和 Host 参与方,Guest 和 Host 参与方执行参数的更新(反向传播阶段);
通过上面的流程可以看到 FATE 的实现与常规的纵向联邦的实现方案基本一致,唯一的差异在于计算反向传播梯度 ∂loss/∂y (上面流程使用常量 d 表示)时没有乘上 2,从而导致 ∂loss/∂w 比预期小一倍,但是常数倍的梯度改变不会影响训练结果,因为参数更新时,都是通过 w -= η * ∂loss/∂w 进行更新,而常量 η 就是控制参数学习速率的,因此 ∂loss/∂w 减少为 1/2 可以等价于 1/2 速率下的学习率。因此只会影响学习速度,不会影响结果。
结论
通过上面的介绍,可以看到一个最简化的纵向联邦学习算法的实现方案,并通过工业级的联邦学习框架 FATE 进行了印证。纵向联邦本身并不算复杂,只是在各方独立训练的模型上执行叠加组合,最终利用各方的参数共同决定最终的结果。如果不同参与方都能提供相关的特征,最终大概率会取得超出单一参与方的效果。