深入探索 FATE 纵向联邦学习安全方案

背景介绍

在之前的 FATE 纵向联邦学习实现探索 介绍了纵向联邦神经网络训练的完整流程，在 深入探索 FATE 纵向联邦学习模型设计方案 详细介绍了纵向联邦神经网络的模型设计方案，但是对于如何在模型训练过程中保证模型的安全性基本都没有深入展开。这篇文章是 FATE 纵向联邦神经网络的最后一篇，补上了安全性这一环。

安全协议

在开始具体的内容的介绍前，需要先了解同态加密以及经典的同态加密实现方案 Paillier。

同态加密是指满足同态性质的加密算法，即用户可以对加密的数据直接进行数学运算，加密数据运算的结果解密后与明文直接运算的结果是相等的。图示如下所示：

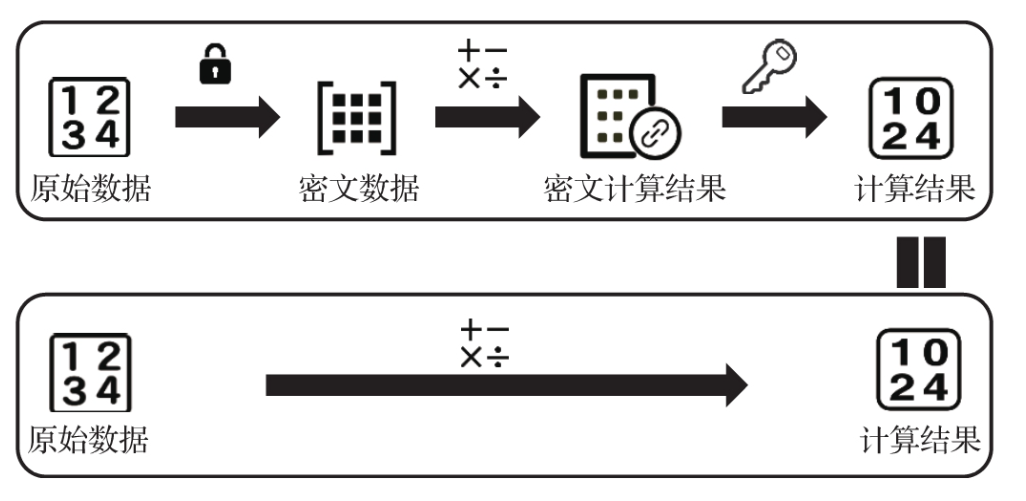
为啥同态加密这么实用呢？可以设想一下，大部分情况下我们都不希望原始数据被其他人知道，但是在多方协作情况下经常会需要数据进行联合操作，但是常规加密的数据没办法进行任何运算，运算后的加密数据就没办法解密了。而同态加密就解决了这个问题，不需要泄露原始信息，多方就进行了联合计算，计算后的结果也可以轻松解密。

Paillier 是一个经典而使用广泛的实现方案，实现的步骤见 Paillier_cryptosystem，在 Python 语言中存在一个使用比较多的库 python-paillier，有兴趣的可以深入了解下。

这边不深入实现细节，只需要了解下 Paillier 初始化时会生成公钥与私钥，公钥用于加密数据，私钥用于解密数据。FATE 的同态加密使用的就是 Paillier 机制。FATE 中多方协作时，所有的参与方都可以进行加密，只有一方可以解密，从现有的实现来看，一般是 Host （不存在标签数据的参与方）具备解密能力。

另外同态加密有一个广泛使用的标记符，一般使用 [] 进行表示。比如原始数据为 a, 其同态加密数据一般表示为 [a]，下面也会直接使用这个标识符。

FATE 安全机制

FATE 在纵向联邦神经网络中的训练过程过程中，个人从是实际的执行流程进行总结，包含了下面三种安全机制，在了解了下面的三种安全机制后，就可以了解 FATE 复杂的纵向联邦神经网络训练流程了。

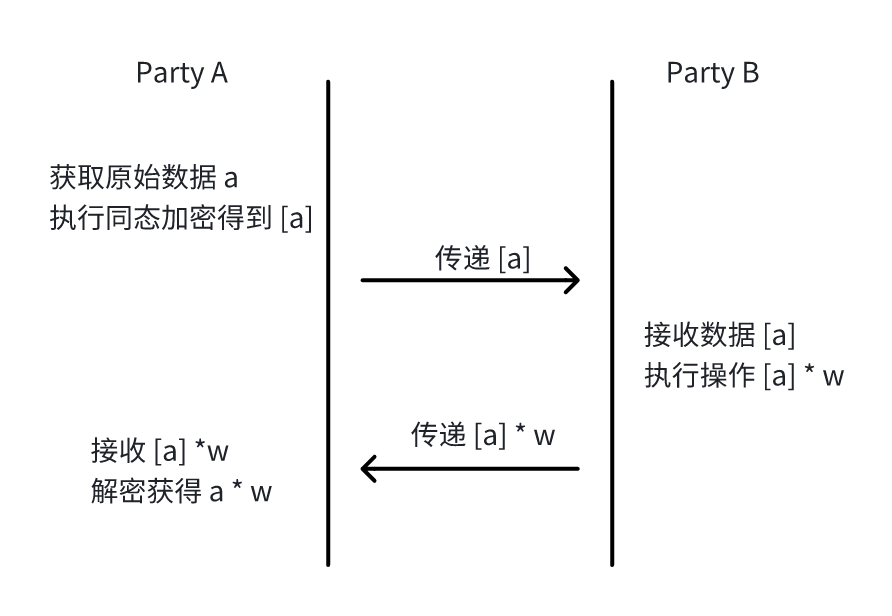
同态加密数据保护（机制 1）

这个安全机制比较直观，参与方为了避免泄露明文的数据，使用同态加密对明文数据进行加密，传递给其他参与方进行运算，然后对运算后的结果直接进行解密，从而实现安全的数据运算。对应的流程如下所示：

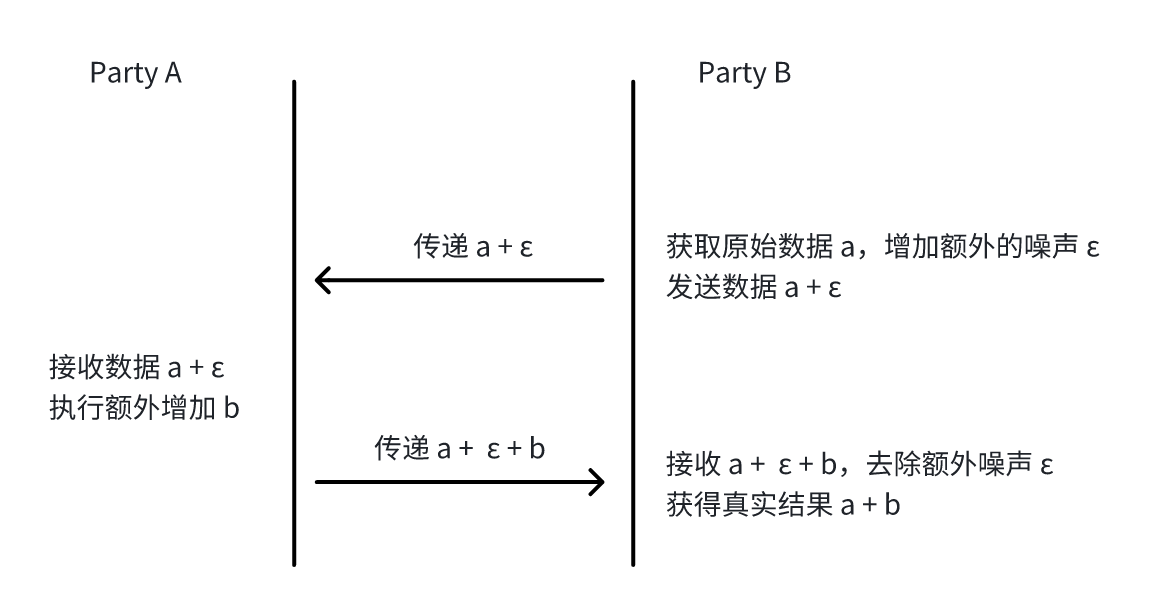
增减噪声数据保护 （机制 2）

发起方在传递数据前，额外增加随机噪声数据，接收方收到数据后，执行必要的运算（预期只有加减运算），然后将处理后的数据发送回来，发起方将接收到的结果减去增加的噪声，即可得到正确的结果。对应的流程如下所示：

累积噪声参数保护机制（机制 3）

这个技术方案相对比较复杂，需要结合前向传播与反向传播。首先看看简化后的流程：

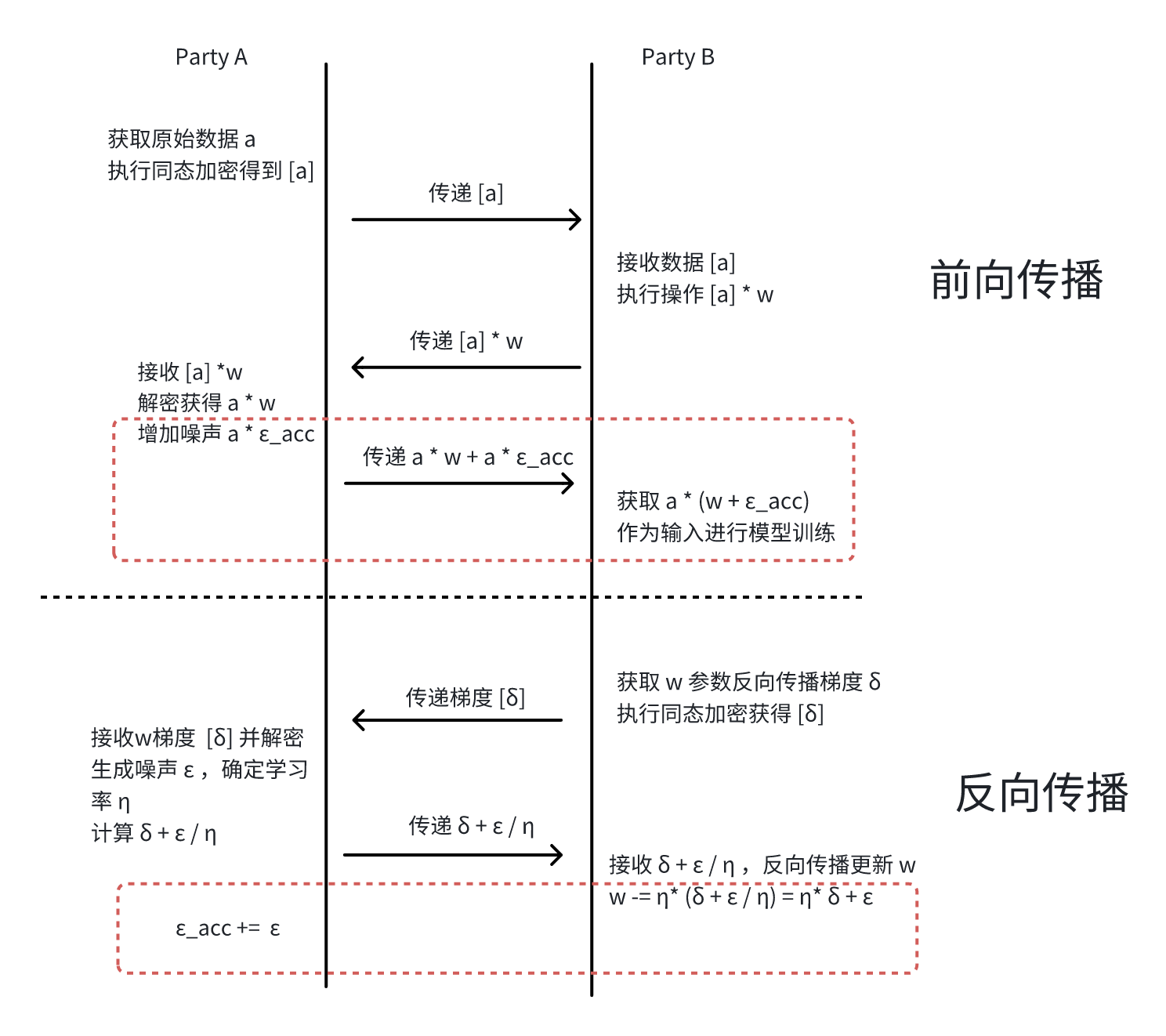
因为机制比较难以理解，我们实际手动执行看看其中数值的变化，从中就可以看到其中此方法的用途：

1. 前向传播第一轮
   • 参与方 Party A 获得的原始数据 a，通过参与方 Party B 执行操作并解密得到 a * w；
   • ε_acc的值被初始化为 0，因此参与方 Party A 实际传递给 Party B 的 (w + ε_acc) * a = w * a，此数据作为 Party B 后续的模型的输入进行训练；
2. 反向传播第一轮
   • 参与方 Party B 获取到 w 参数反向传播的梯度 δ, 常规机器学习会执行 w -= η* δ 实现参数的更新（η 为学习率），但是参与方 Party B 实际额外减去了噪声 ε，执行的是 w -= η* δ + ε，w 比预期少了 ε （注意这一块开始与常规的机器学习的差异，但是后续的动态调整就带来了安全性）
   • 参与方 Party A 将噪声 ε 增加至 ε_acc 中，此时 ε_acc 等于 ε
3. 前向传播第二轮
   • 参与方 Party A 获得原始数据 a, 通过参与方 Party B 执行操作并解密得到 a * w；
   • ε_acc 的值在上一轮被更新为 ε, 因此实际传递的就是 a * (w + ε_acc) = a * (w + ε) ，而 w 在上一轮中比预期减少了 ε，此时加上恰好符合预期（注意这边补上了上一轮 w 的缺失，同时具备对 a 的保护能力，因为参与方 Party B 无法获知 ε_acc 的值）
4. 反向传播第二轮
   • 参与方 Party B 获取到 w 参数反向传播的梯度 δ, 常规机器学习会执行 w -= η* δ 实现参数的更新，此次参与方 Party B额外减去了噪声 ε_2（方便与一轮的噪声 ε 区分开来），执行 w -= η* δ + ε_2，此时 w 比预期少了 ε + ε_2（注意 w 是在上一轮的结果上更新的，因此会差值会累加） -参与方 Party A 将噪声 ε_2 增加至 ε_acc 中，此时 ε_acc 等于 ε + ε_2
5. 前向传播第三轮
   • 参与方 Party A 获得原始数据 a, 通过参与方 Party B 执行操作并解密得到 a * w
   • ε_acc 的值在上一轮被更新为 ε + ε_2，此时实际传递的就是 a * (w + ε_acc) = a * (w + ε + ε_2)，而 w 比预期少了 ε + ε_2，此时加上刚好符合预期（下一轮的前向传播的训练会补上前面多轮 w 的缺失值，同时具备对 a 的保护能力）

通过上面的流程可以看到，复杂的流程主要是为了保护参与方 Party A 中的 a * w，避免 a 被参与方 Party B 获知。因为此数据是作为 Party B 后续模型的输入，而复杂非线性模型无法支持加密下进行训练，因此不能使用同态加密进行保护，只能通过额外的 ε_acc 进行保护。而为了避免 ε_acc 的增加导致模型输入值异常，只能通过 w 在反向传播中提前减少对应的值。这样保证整体的 a * (w + ε_acc) 的值的正确性。

FATE 安全模型训练流程

在 FATE 官方文档 中介绍了纵向联邦神经网络的前向传播与反向传播的完整流程，在理解这个流程前建议先通过 深入探索 FATE 纵向联邦学习模型设计方案 了解其中 FATE 纵向联邦神经网络的模型设计，同时理解上面的 FATE 的三种安全机制，这样才能比较好地理解 FATE 模型训练的流程

下面的流程中 Party A 代表不包含标签数据的 Host 参与方，Party B 代表包含标签数据的 Guest 参与方。下面的流程图完全来自 FATE 官方文档，因为复杂的流程图导致的身体不适请直接联系 FATE 官方进行投诉。

前向传播

FATE 前向传播执行流程如下所示：

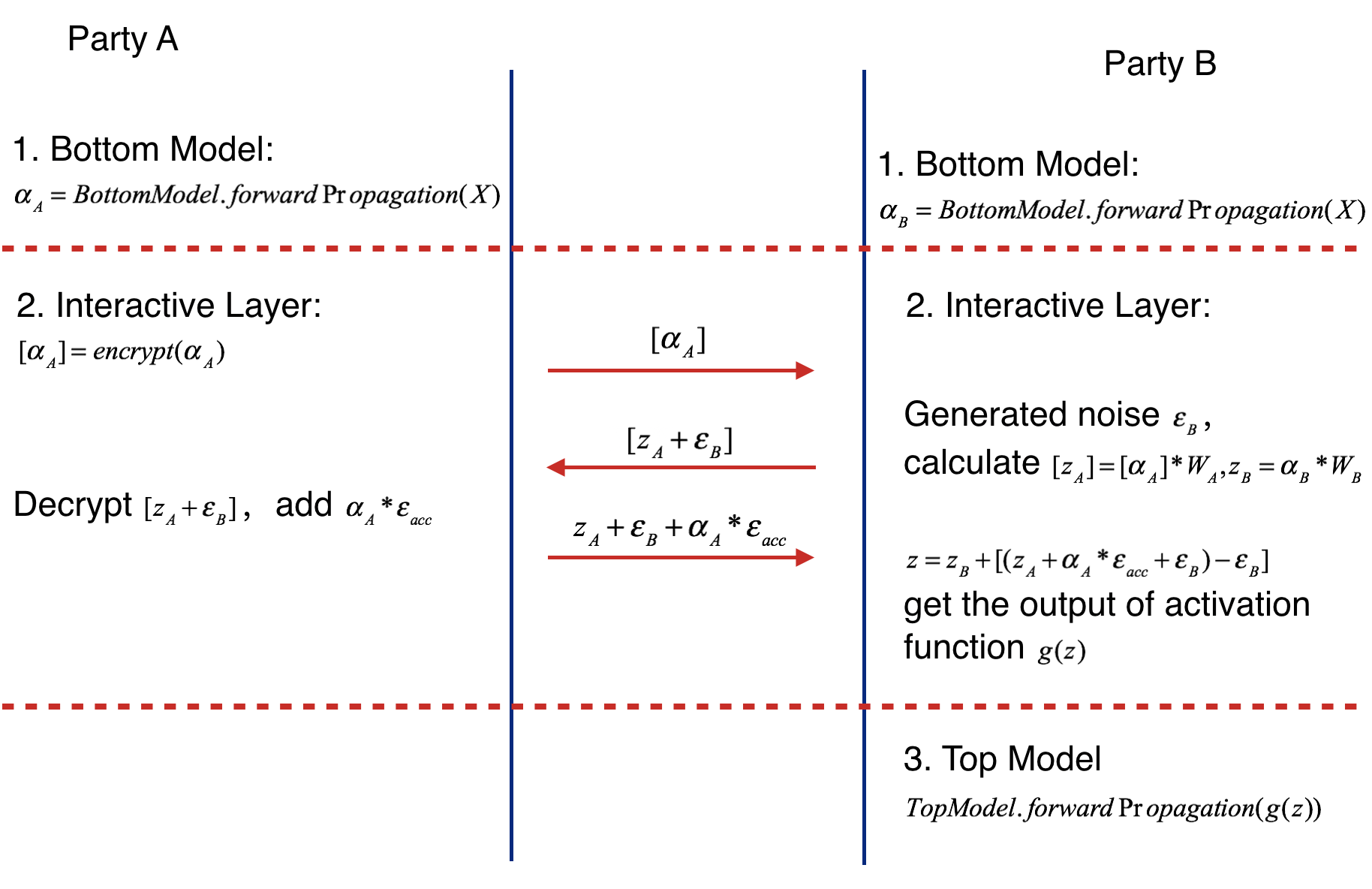
前向传播的过程主要分为三个步骤，分别如下所示：

1. 参与方 Party A 训练的本地模型（Bottom Model） 执行前向传播获得输出 a_A (为了方便文档书写，符号与图示有略微不同，下面都采用类似描述方式)，参与方 Party B 训练的本地模型（Bottom Model） 执行前向传播获得输出 a_B；
2. 第 2 步比较复杂，包含下面的步骤：
   • 参与方 Party A 将本地模型的输出 a_A 使用同态加密转换为 [a_A] 发送给 Party B (后续 Party A 会对经过 Party B 运算后的 [a_A * W_A + ε_B] 执行解密，保护 a_A 避免被 Party B 知道，应用的是上面提到的机制 1)
   • 参与方 Party B 同时会将 a_B 使用全连接层进行线性转换, 得到 z_B = a_B * W_B
   • 参与方 Party B 接收到 [a_A] 使用全连接层进行线性转换得到 [z_A] = [a_A] * W_A，并添加额外的噪声 ε_B，将得到的结果 [z_A + ε_B] 发送给参与方 Party A（此时增加的噪声 ε_B 会在之后传回的结果中直接消除掉，应用的是上面提到的机制 2）
   • 参与方 Party A 会对收到的 [z_A + ε_B] 执行解密得到 z_A + ε_B, 并添加上 a_A * ε_acc，得到 z_A + ε_B + a_A * ε_acc (增加额外的 ε_acc 是为了保护目前明文 z_A，防止参与方 Party B 反向获得 a_A 的数据，应用上面提到的机制 3)
   • 参与方 Party B 将收到的 z_A + ε_B + a_A * ε_acc 与 z_B 取和，完成多个本地模型（Bottom Model）结果的融合，之后去除 Party B 自己添加的噪声 ε_B，得到 z = z_B + z_A + a_A * ε_acc = z_B + a_A * (W_A + ε_acc)，并通过激活函数进行处理得到 g(z) (可以看到机制 2 的应用比较明显，另一方完成计算后立即去除噪声得到真实的数据)
3. 参与方 Party B 将融合了多方特征的输出 g(z) 提供给全局模型(Top Model) 完成模型训练；

反向传播

FATE 反向传播的执行流程如下所示：

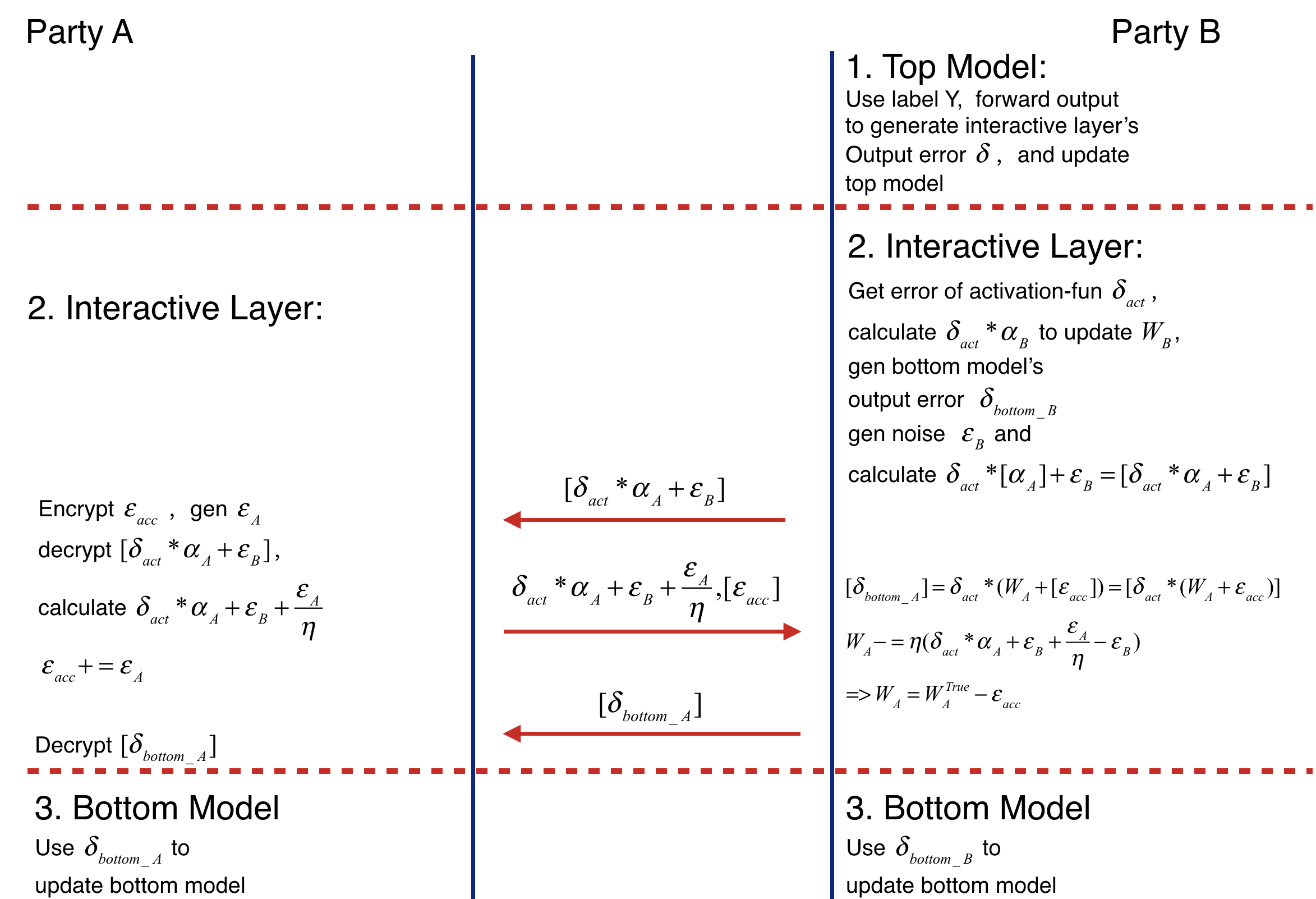
反向传播的过程依旧包含三个步骤，分别如下所示：

1. 参与方 Party B 使用标签 Y 作为前向传播的输出，确定对应的损失，然后更新全局模型对应的参数，并确定全局模型输入对应的梯度 δ;
2. 第 2 步比较复杂，具体如下所示：
   • 参与方 Party B 根据全局模型输入对应的梯度 δ, 进行反向传播，利用链式法则计算激活函数之前的梯度 δ_act，计算参与方 Party B 本地模型对应的梯度 δ_bottom_B
   • 参与方 Party B 生成 δ_act 与 [a_A] 的乘积，并额外增加噪声 ε_B，得到 [δ_act * a_A + ε_B] (这个噪声 ε_B 会在传回结果时直接消除，应用上面的机制 2)
   • 参与方 Party A 生成噪声 ε_A，解密 [δ_act * a_A + ε_B] , 计算得到 δ_act * a_A + ε_B + ε_A / η(这个噪声 ε_A 是为了更新参数 W_A 时额外减少部分内容，方便前向传播时额外传递累加噪声 ε_acc 保护本地模型输出，应用上面的机制 3)
   • 参与方 Party A 加密 ε_acc 得到 [ε_acc]，将前面的 δ_act * a_A + ε_B + ε_A / η 与 [ε_acc] 一起发送给参与方 Party B
   • 参与方 Party B 使用收到的 [ε_acc] 获得参与方 A 本地模型反向传播的梯度 [δ_bottom_A] = δ_act * (W_A + [ε_acc])(注意这是因为前向传播时 z = a_B * W_B + a_A * (W_A + ε_acc)，因此本地模型输出 a_A 对应的梯度就会额外多了 ε_acc)
   • 参与方 Party B 使用收到的 δ_act * a_A + ε_B + ε_A / η 去除噪声 ε_B，更新 W_A 的参数 W_A -= η * (δ_act * a_A + ε_B + ε_A / η - ε_B) = η * (δ_act * a_A) + ε_A (去除噪声 ε_B 避免干扰应用的是机制 2，更新 W_A 时额外减去 ε_A 是应用机制 3)
   • 参与方 B 将计算确定的参与方 A 本地模型反向传播的梯度 [δ_bottom_A] 发送给参与方 A，参与方 A 解密获得 δ_bottom_A (参与方 A 前面发送同态加密的 [ε_acc]，参与方 B 计算出的就是加密后的 [δ_bottom_A]，之后参与方 A 执行解密获得真实数据，应用机制 1)
3. 使用本地模型反向传播的梯度 δ_bottom_A 和 δ_bottom_B 更新本地模型（Bottom Model）;

总结

本文基于 FATE 纵向联邦神经网络的设计，总结其中保护模型与敏感数据的三种机制，这三种机制都是建立在同态加密的基础上。从目前来看，机制 1 与机制 2 可以广泛应用在各个需要进行保护的场景下，而机制 3 则比较适用于联合建模，同时无法使用同态加密保护数据的复杂场景。

• Previous
  深入探索 FATE 纵向联邦学习模型设计方案
• Next
  最简安全纵向联邦学习实现探索